【印刷可能】 y=sin^-1(2x/1 x^2) find dy/dx 321837

If cos −1( x 2y 2x 2−y 2 )=2kshow that y dxdy =xtan 2k If x = 2 c o s e c − 1 t and y = 2 s e c − 1 t ( ∣ t ∣ ≥ 1), then d x d y is equal to Find the derivative of sin − 1 1 x 2 2 x with respect to tan − 1 1 − x 2 2 xIf the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is 6 The locus represented by x y y z = 0 is 7 If f (x) = sin − 1 ( 2 x 1 x 2), then f' ( 3) is 8 If P and Q are symmetric matrices of the same order then P Q − Q P is Use absolute value concept to find the distance between a two points 'S' and 'T' such that, point 'S' is 9 m away from the origin towards right and point 'T' is 2 m away from the origin in the opposite direction b the points 26 and 17

If Y Sin 1 X 2 1 Then Dy Dx

Y=sin^-1(2x/1 x^2) find dy/dx

Y=sin^-1(2x/1 x^2) find dy/dx-Question X Dy/dx Y = 2x^2, Y (1) = 5 (2x 1) Dx (3y 7) Dy = 0 (sin Y Y Sin X0 Dx (cos X X Cos Y Y) Dy = 0 (x Y^3 Y^2 Sin X) Dx = (3xy^2 2y Cos X) Dy (tan X Sin X Sin Y) Dx Cos X Cos Y Dy = 0 (2y^2 3x) Dx 2xydy = 0 Cos X Dx (1 2/y) Sin Xdy = 0 (10 6y E^3x) Dx 2 Dy = 0 (y^2 Rightarrow Yx) Dx X^2 Dy Say if the problem y=sin(axb) Then you can find the derivative of this using chain rule dy/dx = cos(axb)*d/dx(axb) dy/dx = cos(axb)(a) dy/dx = acos(axb) Similarly y=sin(2x1) dy/dx = cos(2x1)d/dx(2x1) dy/dx = cos(2x1)(2) dy/dx=2cos(2x1) Answer

Ex 7 10 3 Evaluate Integrals Sin 1 2x 1 X2 Dx Ex 7 10

Create your account View this answer We have to find dy dx if sin2xsin2y= 1 2 d y d x i f sin 2 ⁡ x sin 2 ⁡ y = 1 2 Differentiate the given equation with respect to x $$\beginFind dy/dx when y = x^2 (cos (x)) y = x 2 (cos (x)) therefore we will need to use the product rule, dy/dx = u dv/dx v du/dx where u = x 2 and v = cos (x) du/dx = 2x and dv/dx = sin (x), (don't forget the negative symbol when differentiating cosine) dy/dx = x 2 ( sin (x)) cos (x) (2x) dy/dx = 2x (cos (x)) x 2 (sin (x)) Answered byFind dy/dx Of Sin2 X Cos2 Y = 1 Get the answer to this question and access other important questions, only at BYJU'S

Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!//googl/JQ8NysLinear Differential Equation cos(x)dy/dx sin(x)y = 1 How to solve a linear differential equation Transcript Ex 53, 9 Find 𝑑𝑦/𝑑𝑥 in, y = sin^(−1) (2𝑥/( 1 2𝑥2 )) 𝑦 = sin^(−1) (2𝑥/( 1 2𝑥2 )) Putting x = tan θ 𝑦 = sin^(−1

Move 2 2 to the left of cos ( 2 x) cos ( 2 x) Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 1 n = 1 Multiply 2 2 by 1 1 Reform the equation by setting the left side equal to the right side Replace y' y ′ with dy dx d y d xInverse Trigonometric Functions IF y = sin1 (2 x1 /14 x) find dy/dx Share with your friends Share 24 y = sin1 2 x 1 1 4 x = sin1 2 x 2 1 2 2 x L e t 2 x = tanSo y=f ( (2x1)/ (x²1)) Differentiating wrt x this you'll get Dy/dx= {f' ( (2x1)/ (x²1))X (x²1) (2) (2x 1) (2x)}/ {x²1} It's given than f'x= (sinx² ) // hope its x² Since f' (of hand) = some other function of hand only Just replacef' ( (2x1)/ (x²1))

If Y Sin 1 X 2 1 Then Dy Dx

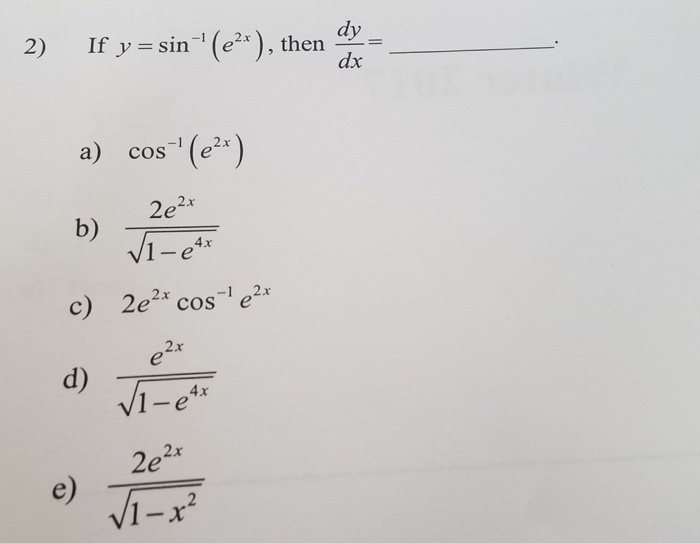
Solved If Y Sin 1 E 2x Then Dy Dx A Chegg Com

If y=cos^1(2xsqrt(1x^2)), find dy/dxWeekly Subscription $249 USD per week until cancelled Monthly Subscription $799 USD per month until cancelled Annual Subscription $3499 USD per year until cancelled1 Problem 1 Give the general solution y0 = x2/y ydy = x2 dx ⇒ 1 2 y2 = 1 3 x3 C 2 Problem 3 Give the general solution to y0 y2 sin(x) = 0 First write in standard form dy dx = −y2 sin(x) ⇒ − 1 y2 dy = sin(x)dx Before going any further, notice that we have divided by y, so we need to say that this is value as long as y(x) 6= 0

How To Find Dy Dx When Y Cos 3cos X 4sinx 5 Quora

Misc 13 Find Dy Dx If Y Sin 1 X Sin 1 Root 1 X2 Miscellaneous

Rewrite the differential equation in the standard form M(x,y)dxN(x,y)dy=0 The differential equation y^2dy\frac{2}{3}xdx=0 is exact, since it is written in the standard form M(x,y)dxN(x,y)dy=0, where M(x,y) and N(x,y) are the partial derivatives of a twovariable function f(x,y) and they satisfy the test for exactness \displaystyle\frac{\partial M}{\partial y}=\frac{\partial N}{\partial x} Find dy/dx if sin^2x cos^2y = 1 vaishnavs296pel6jd vaishnavs296pel6jd Math Secondary School answered Find dy/dx if sin^2x cos^2y = 1 2 See answers ammu300 ammu300 A) (sinx)^2 (cosx)^2=1 do dy/dx= last ansrr dy/dx=sin2x/sin2y seriyano ank kitiath 1/1x^2 ath tan inverse x a cot nu SingGet an answer for '` ` Q If `y =` `(5x) / root(3) ( 1 x^2)` `` `sin^2(2x 3)` Find `dy/dx` ' and find homework help for other Math questions at eNotes

Find Dy Dx In The Following Y Sin 1 2xsqrt 1 X 2 1 Sqrt 2 Lt X Lt 1 Sqrt 2

Calculusstudyguide

 If y=log( base cos x) sinx{log (base sin x) cos x}^1 sin ^1 {2x/(1x^2)} find dy/dx at x = pi/4 Share with your friends Share 19 Dear Student, Please find below the solution to the asked query y = log cosxDifferebtiating this relationship with respect to x , we obtain `d/dx (x) = d/dx (cos y/2)` ⇒ `1 = sin y/2 d/dx (y/2)` ⇒ ` (1)/ (sin y/2) = 1/2 dy/dx` ⇒ `dy/dx = (2)/ (sin y/2) = (2)/sqrt (1 cos^2 y/2)` ⇒ `dy/dx = (2)/sqrt (1If y = 2x sin2x, find dy/dx when x = π/4 If y = 2x sin2x, find dy/dx when x = π/4 A π B π C π/2 D π/2 Correct Answer Option D Explanation y = 2x cos2x sin2x dy/dx = 2 cos2x (2x Past Question and answers for schoolworks

If Y Log Cos X Sin X Log Sin X Cos X 1 Sin 1 2x 1 X 2 Find Dy Dx At X P 4 Sarthaks Econnect Largest Online Education Community

Solved Use Implicit Differentiation To Find Dy Dx In Chegg Com

 So I write y equals the integral of bracket 3x 2 2 dx Now how did I know that, becuase `dy/dx` is 3x 2 2, y must be the integral of 3x 2 2 `dy/dx` differentiation and integration are opposite processes Ok, so I just integrate this and I get `x^3/3`, and there is 3 on the front, so the 3 cancels out so I just get x 3 2x KSolution For Find (dy)/(dx) in the followingy=sin^(1)((2x)/(1x^2)) Find the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5If ` y=sin ^(1)(2x sqrt (1x^(2))),then (dy)/(dx)=`

Y Sin 1 1 2x 2 Then Dy Dx

Ex 7 10 3 Evaluate Integrals Sin 1 2x 1 X2 Dx Ex 7 10

 find dy/dx for y=sin^1(1x^2/1x^2) Brainlyin Find dy/dx for y=sin^1(1x^2/1x^2) 1118 gshindegshinde Math Secondary School answered Find dy/dx for y=sin^1(1x^2/1x^2) 2 Transcript Ex 53, 12 Find 𝑑𝑦/𝑑𝑥 in, y = sin–1 ((1− 𝑥^2)/( 1 𝑥2 )) , 0 < x < 1 y = sin–1 ((1− 𝑥^2)/( 1 𝑥2 )) Putting x = tan θ y2 days ago Can anyone help me solve this problem?

Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5

If Y Sin 2tan 1 1 X 1 X 1 2 Then Find Dy Dx And If 5 X 5 Y 5 X Y Then Prove That Dy Dx 5 Y X 0 Mathematics Topperlearning Com Q011rcnn

 IF y = sin1 (2x1/14x) find dy/dx Maths Inverse Trigonometric Functions NCERT Solutions; (dy)/(dx)=2/sqrt(14x^2) We can use here the formula for derivative of sin^(1)x, which is d/(dx)sin^(1)x=1/sqrt(1x^2) As such to find derivative (dy)/(dx) for y=sin^(1)2x using chain rule is given by (dy)/(dx)=1/sqrt(1(2x)^2)xxd/(dx)(2x) = 2/sqrt(14x^2) Find dy/dx, if y=sin1 x √(1x)√x √(1x 2) differential equations;

If Y Cos M Cos 1 X Show That 1 X 2 Y

Differentiate The Following With Respect To X Sin 1 2 X 1 3 X 1 36 X Sarthaks Econnect Largest Online Education Community

Find dy/dx y=sin (x)^2 y = sin2 (x) y = sin 2 ( x) Differentiate both sides of the equation d dx (y) = d dx (sin2(x)) d d x ( y) = d d x ( sin 2 ( x)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Differentiate using the chain rule, which states that d d xNCERT Solutions, Sample Papers, Notes, Videos Install Now dy/dx=x (2logx1)/sinyycosy Report Posted by Meenakshi Rajput 4 years, 2 months ago CBSE > Class 12 > Mathematics 1 answers Sahdev Sharma 4 years, 2 months ago d y d x = x ( 2 l o g x 1) s i n y y c o s y if y = (1 sin2x/1 sin 2x) 1/2 show that dy/dx sec 2 (π/4 – x) = 0 donot go shortcut if y = log tan (∏/4 x/2) show that dy/dx = sec x donot go shortcut if y = log (x (1 x 2 ) 1/2 ) prove that dy/dx = 1/log(x (1 x 2 ) 1/2 ) 1/(1 x 2 ) 1/2

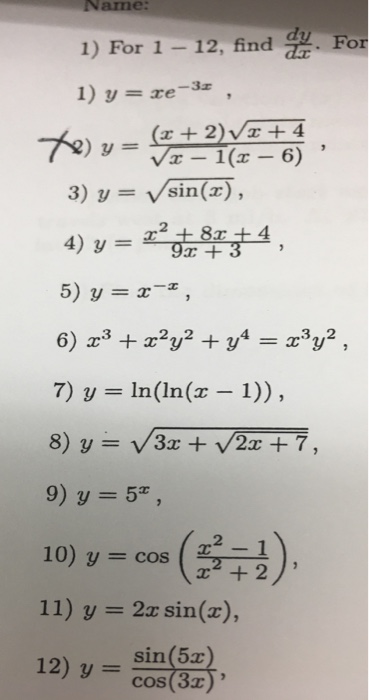
Solved 1 For 1 12 Find Dy Dx For 1 Y Xe 3x 2 Y Chegg Com

If Y Sin 1 X 2 1 X 2 1 Sec 1 X 2 1 X 2 1 Then Dy Dx Is Equal To Youtube

Answer to Let y=(x^{2}1)^{2}e^{2x} Find dy/dx By signing up, you'll get thousands of stepbystep solutions to your homework questions YouSo y = sin − 1 (1 tan 2 θ 2 tan θ ) = sin − 1 (sin 2 θ) = 2 θ = 2 tan − 1 (2 x) Differentiating on both sides d x d y = 1 ( 2 x ) 2 2 × 2 x ln 2 = 1 4 x 2 x 1 ln 2 Get an answer for '`tan^1(x^2 y) = x xy^2` Find `(dy/dx)` by implicit differentiation' and find homework help for other Math questions at eNotes

Find Dy Dx X Cos 1 1 1 T2 1 2 Y Sin 1 T 1 T2 1 2 Explain In Great Detail Mathematics Topperlearning Com 6ebbrcqq

If Y Sin 1 2x 1 X 2 Then Dy Dx Is Equal T

1 Consider the curve y=x^2 a write down (dy)/(dx) My answer 2x The point P(3,9) lies on the curve y=x^2 b Find the gradient of the tangent to the curve at P My answer 2*3=6 c Find the equation of the normal to the curve can you please explain how to to find dy/dx for the function x^2 y Y^2 x = 2 asked in CALCULUS by mathgirl Apprentice differentiation;Y Sin 1 2x 1 X 2 Find Dy Dx;Find Dy Dx If Y Sin 1 2x 1 X 2 hviezdoslavov kubín 7 ročník hugolin gavlovic valaska skola mravov stodola if f x x 3 x 2 x 1 then f 2 humanizmus a renesancia znaky ii rákóczi ferenc portr4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this question we need to sub

If Y Cos 1 1 X 1 X Then Find Dy Dx Youtube

4cugd7yqaila6m

Let's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc If y = sin^1 (2x√(1x^2), 1/√2 ≤ x ≤ 1/√2, then dy/dx is equal toStart your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero Cancel

3

3

Log y = log (x1)log (x2) 1/2log x 1/ydy/dx = 1/ (x1) 1/ (x2) 1/2x dy/dx= y 2x (x2)2x (x1) (x1) (x2)/2x (x1) (x2) dy/dx = { (x1) (x2)/√x} 2x^2–4x2x^2–2xx^23x2/2x (x1) (x2) dy/dx = (3x^2–3x2)/2x√x Answer 4K views View upvotes\begin{align}(1 \frac{x^3}{y} \sin^2x)dx \frac{1}{y}(x \frac{1}{\cos^2(2y)})dy = 0\end{align} Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and buildCOMEDK 08 If y = sin1 ((5x12 √1 x2/13)) , then (dy/dx) = (A) (3/√1 x2) (B) (12/√1 x2) (1/√1 x2) (D) (1/√1 x2) Check A

If Y X Sin 1 X Sqrt 1 X 2 Find Dy Dx Youtube

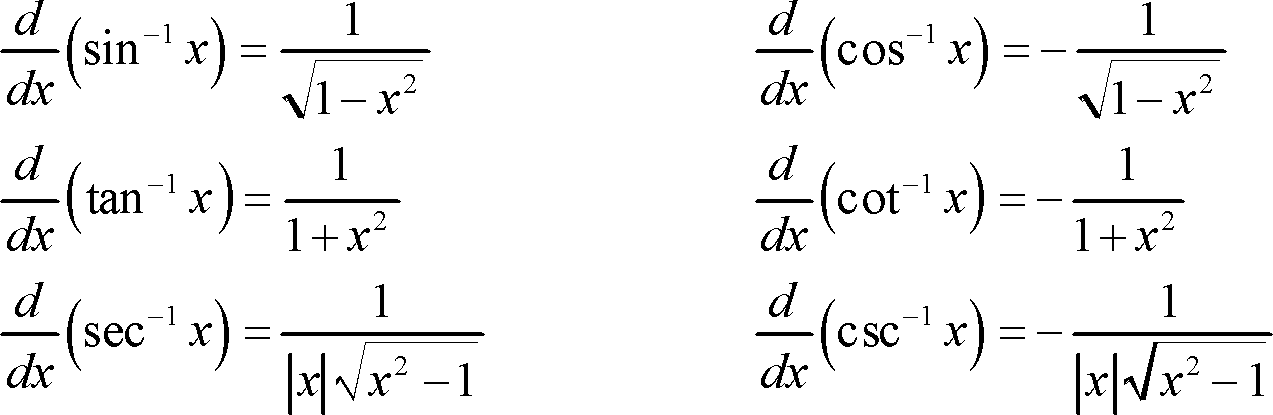
How Do You Find The Derivative Of Sin 1 2x 1 Socratic

 Find dy dx d y d x, when y = sin ( 1 x2 1 − x2) y = s i n ( 1 x 2 1 − x 2) dy/dx, y = sin (1 x2)/ (1 x2) differentiation class12 Please log in or register to add a commentI'm not absolutely sure on how I can deal with this problem with this problem Find $ \dfrac{dy}{dx} $ if $ y = 2u^2 3u $ and $ u = 4x 1 $ I am trying to use the chain rule on it $$ \dfraFind dy/dx of ,y=1/sin(2x/1x^2) Ask questions, doubts, problems and we will help you

Solved Cos X Dy Dx Y Sin X 1 Y Pi 4 0 Solve By Chegg Com

Y Sin 1 Sqrt 1 X Sqrt 1 X 2 Then Dy Dx Youtube

Multiply by 2 to get y 2 = x 2 2x 16 Finally take a square root to obtain Example Find the equation of the function that has the following properties Slope = y sin x and passes through the point (0,2) Solution Since the slope is the derivative, we have dy / dx = y sin x Separating gives dy = sin x dx y Integrating both sides givesPlease Subscribe here, thank you!!!1)Find dy/dx by implicit differentiation x2 − 6xy y2 = 6 y' = 2)Find dy/dx by implicit differentiation 5y sin (x2) = 9x sin (y2) y' = 3)Find y'' by implicit differentiation x2 5y2 = 5 y'' = 4)Use implicit differentiation to find an equation of the tangent line to the curve at the given point x2 y2 = (2x2 4y2 − x)2 (0, 025

1

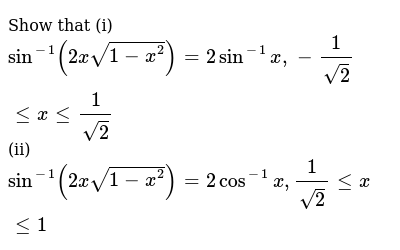
Show That I Sin 1 2xsqrt 1 X 2 2sin 1 X 1 Sqrt 2 Lt Xlt 1 Sqrt 2 Ii Sin 1 2xsqrt 1 X 2 2cos 1 X 1 Sqrt 2 Lt Xlt 1

Share It On Facebook Twitter Email 1 Answer 0 votes answered by rubby (521k points) selected by Vikash Kumar Best answer We have given

Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6

Derivatives Of Inverse Trigonometric Functions Sin 1 2x Cos 1 X 2 Tan 1 X 2 Sec 1 1 X 2 Youtube

Y Sin 1 2x 1 X 2 Find Dy Dxif Dy Dx 2cos 1xthis Is Class 12 The Problem Plz Help Brainly In

Solved Find Dy Dx If Y Ln X 3 2 Squareroot X 2 1 Find Chegg Com

Y Cos 1 3x 4 1 X 2 5find Dy Dx Brainly In

If Y Cos 1 2x 1 X 2 Then Find Dydx

Find Dy Dx In The Following Y Sin 1 2x 1 X 2

If Y Sin M Sin 1 X What Is The Value Of D 2 Y Dx 2 At X 0 Youtube

If Y Sin 1 2x1 X 2 Sec 1 1 X 21 X 2 Show That Dydx 4 1 X 2

How To Find Dy Dx When Y Sin X 2 Y 2 Quora

How To Find Dy Dx Of Sin 1 2x And Y Sin 1 2x 3 Quora

How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora

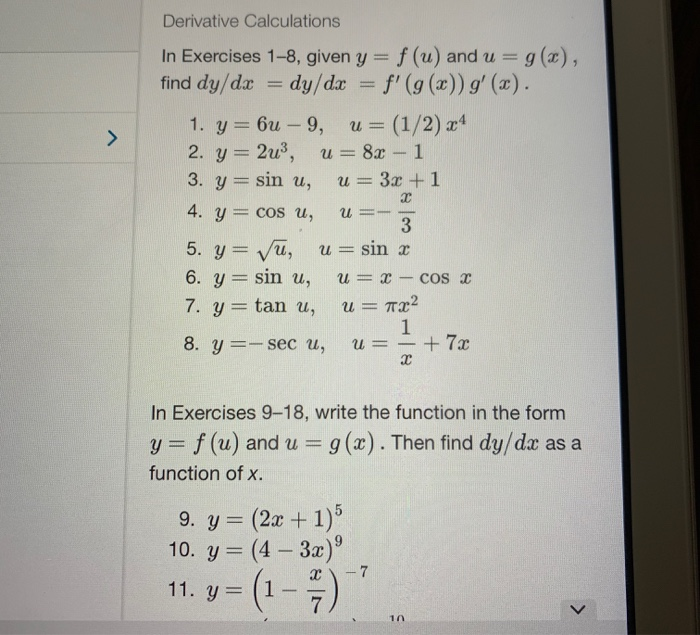
Solved 1 6 Write The Composite Function In The Form F G X Chegg Com

Diferentiate Wrt X If Y Sin 2 Tan 1 1 X 1 X 1 2 Show That Dy Dx X 1 X2 1 2 Mathematics Topperlearning Com 6g8c5y

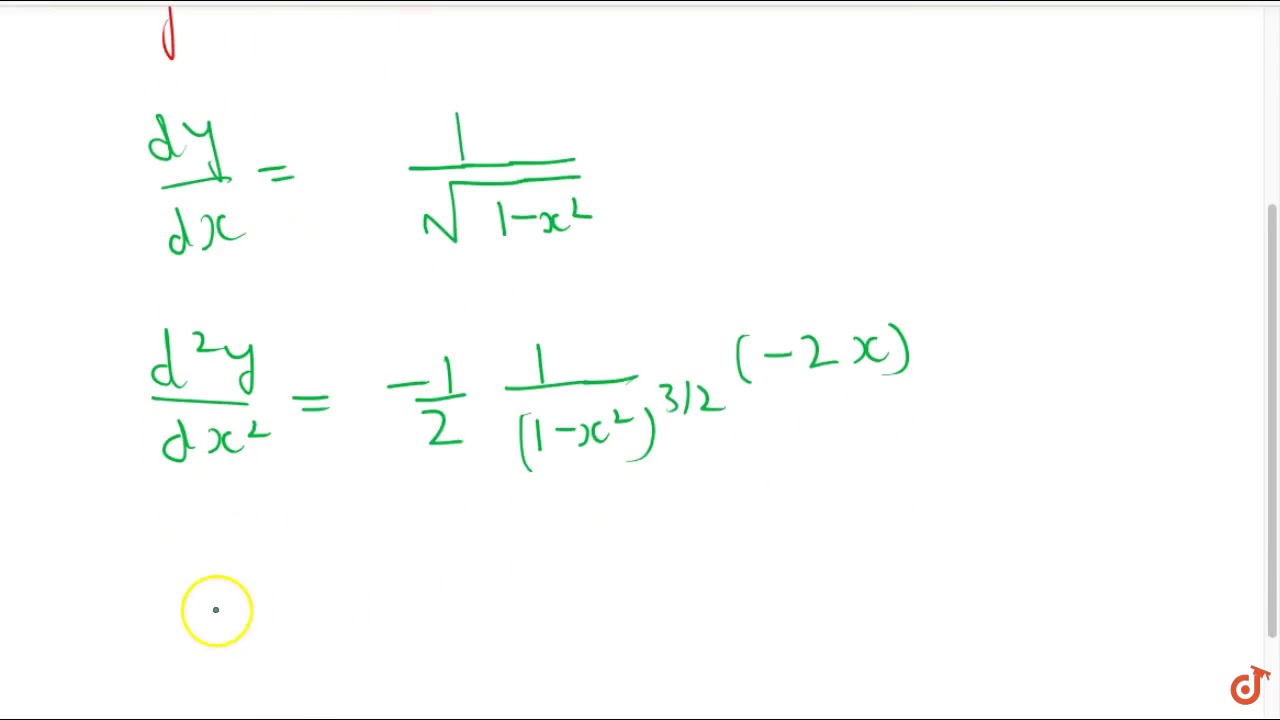
If Y Sin 1 X Then Show That 1 X 2 D 2y Dx 2 X Dy Dx 0 Youtube

If Y F 2x 1 X 2 1 And F X Sinx 2 Can You Find Dy Dx Quora

Find The Value Of D Dx Sin 1 3x 2 X 3 2 And The Other Questio Askiitians

Ex 5 3 10 Find Dy Dx In Y Tan 1 3x X3 1 3x2 Ex 5 3

Solved Please Only Need Help With 1 11 22 33 44 55 Chegg Com

Solved Dy Dx For The Following Fourteen Problems Find Chegg Com

How To Find Dy Dx Of Sin 1 2x And Y Sin 1 2x 3 Quora

Example 41 If Y Sin 1 X Show That 1 X2 D2y Dx2 X Dy Dx 0

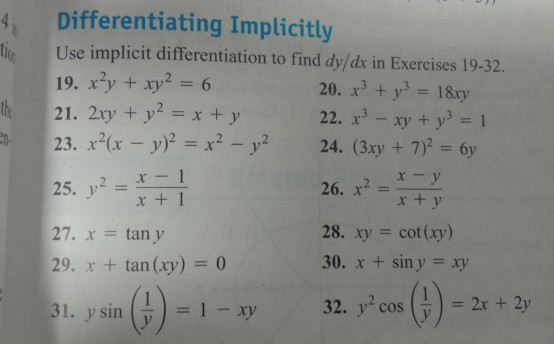
Solved Differentiating Implicitly Use Implicit Chegg Com

If Y Sin 1 X 1 X2 1 2 Show That 1 X2 D2y Dx2 3x Dy Dx Y 0 Explain In Great Detail Mathematics Topperlearning Com Wa3tv55

Q36 If Y Sin 1 5x 12 1 X 2 13 Find Dy Dx Youtube

How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic

What Is The Nth Derivative Of Sin Inverse 2x 1 X 2 Quora

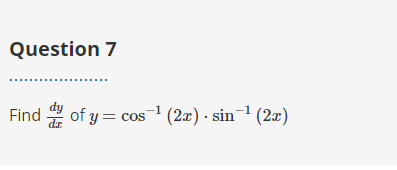
Solved Question 7 Find Dy Of Y Cos 1 2a Sin 1 2a Chegg Com

Ex 9 4 9 Find General Solution Dy Dx Sin 1 X Chapter 9

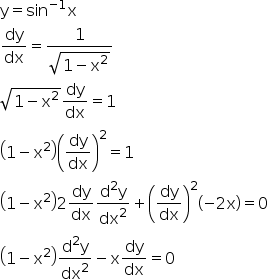
If Y Sin 1 X Prove That 1 Ndash X2 D2y Dx2 Ndash X Dy Dx 0 Explain In Great Detail Mathematics Topperlearning Com Psl1owbb

If Y Sin 1x 2 Cos 1x 2 Then Prove That 1 X 2 D 2y Dx 2 X Dy Dx 4 Sarthaks Econnect Largest Online Education Community

Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5

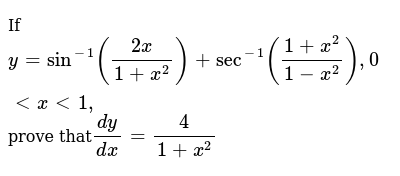
If Y Sin 1 2x 1 X 2 Sec 1 1 X 2 1 X 2 0ltxlt1 Prove That Dy Dx 4 1 X 2 B X 1

If Y Sin 1 X Sqrt 1 X Sqrtx Sqrt 1 X 2 And Dy Dx 1 2 Sqrt X 1 X Youtube

If Y Sin 1 2x 1 X 2 Sec 1 1 X 2 1 X 2 0ltxlt1 Prove That Dy Dx 4 1 X 2 B X 1

B1 6 Derivatives Of Inverse Trig Functions Ppt Download

How To Differentiate Sin X 2 1 Using First Principle Quora

Find Dy Dx Y Sin 1 2x 1 X 2 Sarthaks Econnect Largest Online Education Community

Solved Derivative Of Trigonometric And Inverse Trigonometric Functions Find Dy Dx 1 Y Sin X2 3x 1 2 Y Cos 2 2x 1 3 Y Tan Vx2 Course Hero

If Y Sin 1 X 2 Then Prove That 1 X 2 D 2y Dx 2 X Dy Dx 2 0 Sarthaks Econnect Largest Online Education Community

How To Find Derivative Of Y Sin 2x 1 X 2 Quora

Derivative Of Sin 1 X W R T Cos 1 Sqrt 1 X 2 Is Youtube

Find Dy Dx If Y Sin 1 X 1 X X 1 X 2 Sarthaks Econnect Largest Online Education Community

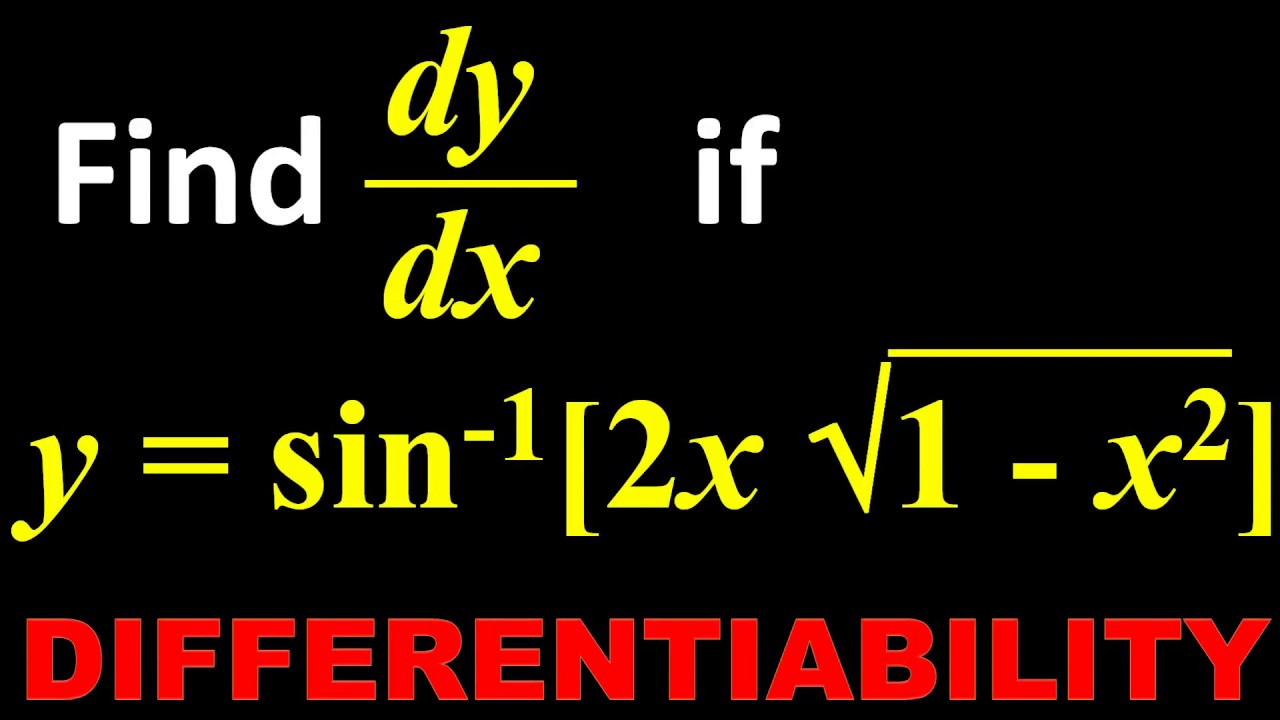
15 Derivative Find Dy By Dx Of Y Sin 1 2x Under Root 1 X2 Youtube

Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6

Find Dy Dx Of Y Sin 1 2x 1 X 2 1 2 Less Than X Less Than 1 2 Youtube

If Y Sin 1 5x 12 1 X 2 1 2 13 Find Dy Dx Mathematics Topperlearning Com Otpu9qyy

If Y Cos 1 2 X 1 1 4 X Fin Dy Dx Sarthaks Econnect Largest Online Education Community

Solved Assignment 1 If Y Xsinx Find Dx Dy 2 If Y Chegg Com

Solved Find The Derivative Of The Function Y X Chegg Com

Find Dy Dx Y Sin 1 2x 1 X 2 1 2 X 1 2 Sarthaks Econnect Largest Online Education Community

Ex 5 3 12 Find Dy Dx In Y Sin 1 1 X2 1 X2 Chapter

If Y Sin 2 Sin 1 X Show That 1 X 2 D 2y Dx 2 X Dy Dx 4y Sarthaks Econnect Largest Online Education Community

Example 41 If Y Sin 1 X Show That 1 X2 D2y Dx2 X Dy Dx

Solved Find The Derivative For The Following Functions Find Chegg Com

If Y Sin A Sin 1 X How Do You Prove That 1 X 2 D 2y Dx 2 X Dy Dx A 2y Quora

Example 3 Show That Sin 1 2x 1 X 2 2 Sin 1 X Class 12

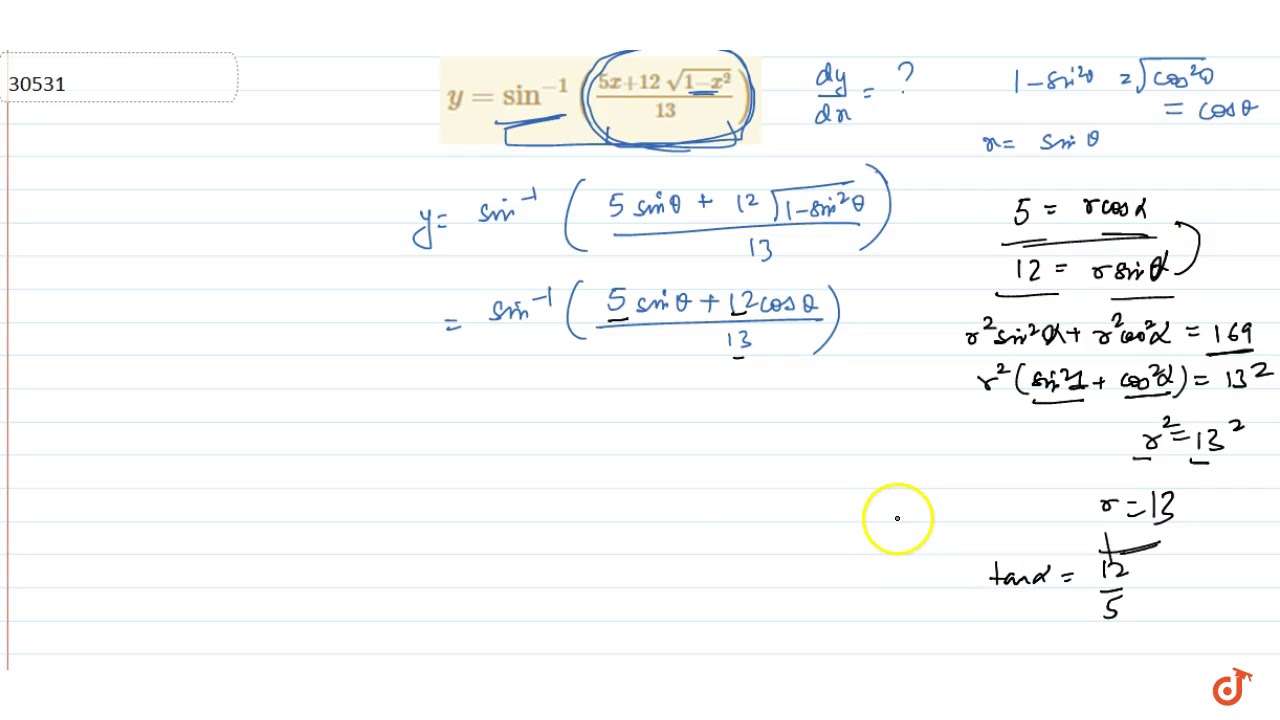
Y Sin 1 5x 12sqrt 1 X 2 13 Youtube

Ex 5 3 13 Find Dy Dx In Y Cos 1 2x 1 X2 Ncert Ex

If Y Sin 2sin 1 X Then Dy Dx Youtube

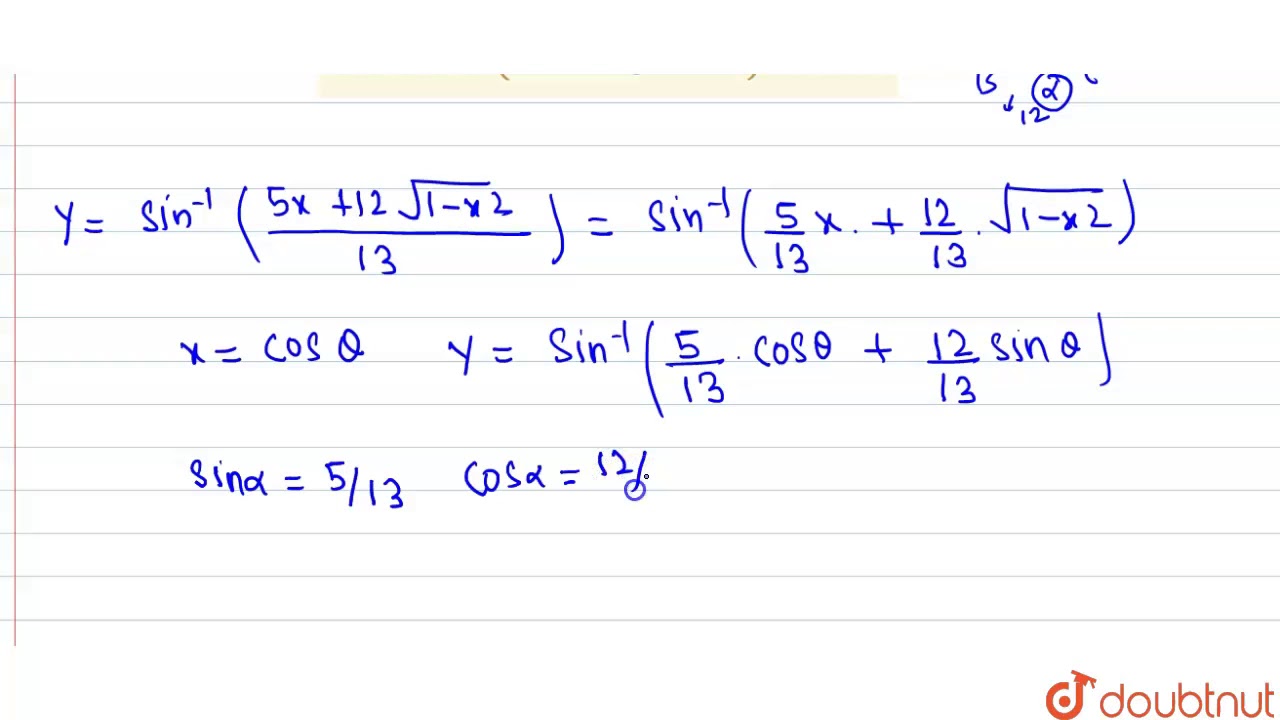
If Y Sin 1 5x 12 Sqrt 1 X 2 13 Find Dy Dx Youtube

Y Cos 1 3x 4 1 X 2 5find Dy Dx Brainly In

1

Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6

If Y Cos 1 2x 3 1 X 2 13 Then Find Dy Dx Sarthaks Econnect Largest Online Education Community

Solved Find The Derivative Of The Following Functions Using Chegg Com

Implicit Differentiation Advanced Example Video Khan Academy

Solved 3 Find Dy Y Sin 7x2 5 A 14x Sin 7x2 5 B Chegg Com

Solved 2 X Arctan X And B F X Differentiate A Y Mple 5 Chegg Com

Solved Find Dy Dx By Implicit Differentiation Sin Y Y Chegg Com

D Dx Sin 1 3x X 3 2 Youtube

If Y Sin 1x 2 Then Show That 1 X 2 D 2ydx 2 X Dydx 2

Ex 5 3 14 Find Dy Dx In Y Sin 1 2x Root 1 X2 Cbse

Iit 19 Find Dy Dx If Y F 2x 1 Square X 1 And F X Sin Square X Youtube

Find Dy Dx Of The Following I Y Sin 1 2x 1 X 2 Ii Y Tan 1 3x X 3 1 3x 2 Sarthaks Econnect Largest Online Education Community

If Y Sin 1 2x Sqrt 1 X 2 Then Dy Dx Youtube